Con "Paradojas geométricas" nos referimos a un tipo clásico de acertijo en el que, al reordenar las piezas que forman una figura, parece perderse parte de su superficie o alguno de sus elementos.

(Cromo de cigarrillos de la marca Gallaher, 1933. Fuente: colección propia).
La primera paradoja geométrica relacionada con el área parece que fue casual y data de de 1566, cuando Sebastiano Serlio en su "Libro primo d'architettura" facilitaba un truco para, a partir de un tablero de 3x10, conseguir uno de 7x4 (en el blog de Mariano Tomatis hay una traducción del texto al inglés). Esta es la imagen original:

(Fuente: Google Books)
Aunque es más intuitivo si comenzamos con el tablero original, formado por dos grandes triángulos que se desplazan. Lo llamativo es que Serlio no se percató de que al formar el rectángulo de 4x7 sobraban dos triángulos de 3x1 por lo que el área total ¡pasaba de ser 30 a ser 31!

(Elaboración propia a partir de la imagen original)
Según cuenta Greg N. Frederickson (en su libro "Dissections: Plane & Fancy", la "biblia" de los problemas de disecciones) al año siguiente otro arquitecto italiano, Pietro Cataneo, publicó el error de Serlio al tiempo que planteaba una alternativa al problema original de Serlio que no presentaba paradoja alguna.
Pero la popularidad de las paradojas geométricas llegó a finales del S.XVIII cuando William Hooper publicó en sus "Rational Recreations" la que desde entonces se conoce como paradoja de Hooper:

(Fuente: Google Books)
Partiendo de la cuadrícula 3x10, cortamos por la diagonal así como por los segmentos EF y GH. Reagrupando los trapecios por un lado y los triángulos por otro, se forman dos figuras cuyas áreas suman 20+12=¡32!
Hoy parece claro que Hooper obtuvo esta paradoja de las Nouvelles récréations physiques et mathématiques de Edmé Gilles Guyot publicadas en 1769:

Hasta tal punto llegó la inspiración que, como bien explica Mariano Tomatis, Guyot puso en la primera edición una figura incorrecta que Hooper repitió, y, cuando el primero corrigió el error, también lo hizo el segundo. Esta es la figura incorrecta, con el segundo rectángulo demasiado grande.

(Fuente: Google Books)
Otra paradoja geométrica famosa es la del "tablero de ajedrez". Al diseccionar adecuadamente un cuadrado de lado 8 puede reordenarse en un tablero de 13x5. Parece que quien la publicó en primer lugar fue probablemente Oskar Schlömilch en 1868:
Fuente: Google Books
Aunque hay dudas de si alguno de los grandes creadores de acertijos pudo ser el verdadero creador de la paradoja. La imagen siguiente se encontraba entre los papeles de Lewis Carroll y su sobrino y biógrafo oficial Stuart Dodgson Collingwood lo incluyó en el libro "Lewis Carroll Picture Book" como uno de sus acertijos favoritos.

(Fuente: Archive.org)
Por lo que se sabe, Carroll debió ocuparse del problema en sus últimos años, hacia 1890, por lo que no sería el autor del mismo, si bien lo generalizó mediante ecuaciones que facilitaban las posibles dimensiones que podían tener los cuadrados que admitieran disecciones de este tipo. Dichas ecuaciones han sido estudiadas por Warren Weaver en el artículo "Lewis Carroll and a geometrical paradox" (American Mathematical Monthly, abril 1938).
El otro genio de los acertijos que, él sí, se declaró autor del acertijo fue Sam Loyd, si bien Loyd es tan conocido por su talento para crear acertijos como por su facilidad para sacarles provecho, por lo que hay que poner en dato en entredicho. En su Cyclopedia aparece una versión de la paradoja y en el texto se explicita que Loyd lo presentó en el American Chess Congress de 1958 (10 años antes de la publicación de Schlömilch). Hay testigos de la presencia de Loyd en ese congreso (¡con sólo 17 años!) pero nadie recuerda que presentara ese acertijo.

(Fuente: Mathpuzzle)
Al menos en la Cyclopedia sí que se añade una segunda solución (parece que debida a Sam Loyd Jr., editor del caótico libro) en la que, en lugar de los 65 rectángulos, se obtienen ¡63!

(Fuente: Mathpuzzle)
Otro gran "monstruo" de los acertijos, Henry E. Dudeney, introdujo esta curiosa versión de la paradoja del tablero de ajedrez en su libro "Amusements in Mathematics": cortado el tablero en diagonal, deslizamos las dos mitades y recolocamos el pequeño triángulo marcado como C, con lo que de nuevo perdemos una unidad de superficie, de 64 a 63.
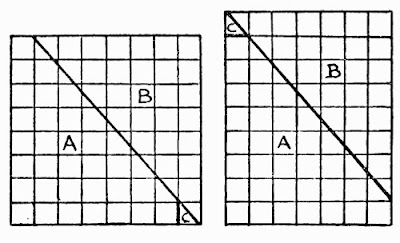
(Fuente: The Project Gutenberg)
Loyd incluye en su Cyclopedia una versión más historiada (y más difícil de descubrir pues utiliza un cuadrado de lado 24) de esta idea, que dice haber planeado en su más tierna juventud, por lo que de nuevo arroja dudas sobre si fue el primero en plantearla.

(Fuente: Mathpuzzle)
Donde no cabe duda de la aportación de Sam Loyd al género es en el capítulo de paradojas donde desaparece un personaje. En 1896 publicó el que es quizá el más famoso puzzle de desaparición: "Get off the earth" (al girar el planeta un cierto ángulo, uno de los hombrecillos desaparecía). Para muchos (entre ellos Gardner) es la mayor creación de Loyd. Se vendieron más de 10 millones de ejemplares del puzzle y hasta se utilizó para la campaña presidencial de William McKinley.

Loyd ideó otros puzzles similares en los que cambiaban los personajes y que pueden verse en su página oficial.
El otro gran tipo de paradoja geométrica de desaparición es la que suele llamarse Paradoja de Deland pues fue patentada por el mago Theodore Deland Jr. en 1907.
Al intercambiar las dos piezas de abajo, una carta desaparece. El ajuste dista mucho de ser muy preciso y además da la impresión de no ser tan original, dado que el que mostramos a continuación, según el experto en puzzles mecánicos Jerry Slocum, data de 1880:
Al reordenar las cuatro piezas que forman la imagen se pueden ver de forma sencilla 8, 9 o 10 huevos (pueden verse estas reorganizaciones en el blog de Mariano Tomatis o en Rob´s Puzzles Page). En la tarjeta también se asegura que se pueden formar 6, 7, 11 o 12 huevos pero quizá siendo más flexible con la forma de colocación (superponiendo piezas o ignorando algunas de ellas).
Se inspirara o no en la de los huevos que desaparecen, la paradoja de Deland sirvió de inspración para otras muchas durante el pasado siglo. Una de las más conocidas y que sirvió para revitalizar este tipo de acertijo fue la de los duendes que desaparecen, "The Vanishing Leprechaun", recogida por Gardner en "¡Ajá! paradojas que hacen pensar" en los años setenta pero que había sido elaborada en 1968 por Pat Lyons.
Era un dibujo formado por 15 duendes y, al intercambiar las piezas superiores, desaparecía uno de ellos. Lo que no sabíamos es que también se puede reorganizar de forma que ¡quedan 13!, tal y como se demuestra en este vídeo de yuikubo10.
Efectivamente, si a partir de la disposición de los 14 duendes, prolongamos la línea vertical que separa las piezas superiores, y dividimos la inferior en otras dos que intercambiamos, se generan 13 (casi perfectos).
Pero el propio Gardner en un libro anterior, "Mathematics, magic and mistery" (1956) ya había tratado a fondo el tema de las paradojas geométricas destacando el trabajo de Mel Stover, quien realizó varias versiones de la paradoja de Deland, entre las cuales quizá la más famosa sea la de los lápices, rescatada años después por Cliff Pickover.

(Fuente: Reality Carnival)
En el mismo libro de Gardner se habla del trabajo de Paul Curry, un mago que realizó otra de las paradojas geométricas más conocidas (en realidad, una especie de término medio entre las de pérdida de área y las de desaparición de un elemento), la que lleva su nombre.
(Fuente: Wikipedia)
De los autores recientes, el que ha realizado sin duda un trabajo más interesante es Gianni Sarcone, quien ha realizado varias elegantes versiones de la paradoja de Deland, así como esta estupenda"Gallina mágica" que hubiera encantado a Curry.

(Fuente: Archimedes´Lab. Autorizado su uso no comercial)
En fin, aún dejándonos algunos ejemplos en el tintero, sólo queda añadir que si uno quiere realizar su propia paradoja geométrica lo tiene fácil, basta trazar unas líneas paralelas, cortar en diagonal y reajustar para perder una de ellas.

Esa "facilidad" se demuestra en que la paradoja trasciende al mundo de los juegos de lógica. Así, tanto Julio Cortázar en el segundo tomo de "La vuelta al día en ochenta mundos" como Martin Gardner en "¡Ajá! paradojas que hacen pensar", cuentan historias de falsificadores que trataron de, a partir de estos trucos, cortar billetes originales en pedacitos que luego pegaban, dejando fuera uno de ellos que luego servía para generar un billete extra.
Para que luego digan que la geometría no da dinero...
(Esta entrada participa en el Carnaval de Matemáticas edición 2.8. Además es uno de los primeros documentos que vamos a generar en el difícil pero apasionante reto de escribir una "Historia de la Matemática Recreativa").











